The concept of relative atomic mass is a cornerstone in the field of chemistry, serving as a fundamental aspect of understanding chemical elements and their interactions. This measure provides insight into the average mass of atoms of an element, taking into account the distribution of isotopes and their respective abundances. Calculating the relative atomic mass is a critical skill for students, educators, and professionals in the sciences, offering a deeper comprehension of the atomic world and its principles. This article aims to demystify the process of calculating relative atomic mass, presenting a thorough guide enriched with examples, applications, and the theoretical underpinnings that frame this essential chemical concept.
Understanding Relative Atomic Mass
Relative atomic mass, often denoted as Ar, is the weighted average of the masses of the isotopes of an element, scaled relative to carbon-12 (12� 12C), which is defined as having a mass of exactly 12 atomic mass units (amu). This concept hinges on the understanding that most chemical elements exist as a mixture of isotopes — variants of the element with the same number of protons but different numbers of neutrons. Each isotope contributes to the overall relative atomic mass of the element based on its natural abundance and individual mass.
The relative atomic mass takes into account these variances, offering a singular value that represents an average mass of the element’s atoms, reflective of the isotopic composition found in nature. This value is crucial for various calculations in chemistry, including stoichiometry, molecular mass determinations, and in understanding reaction mechanisms and material properties.
The Calculative Process
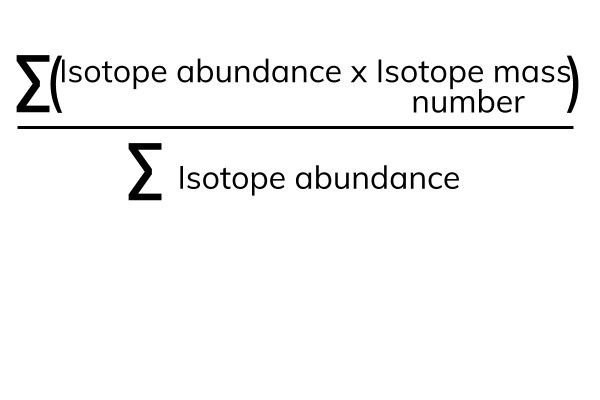
The calculation of relative atomic mass is a straightforward process that involves multiplying the mass of each isotope by its relative abundance (expressed as a fraction), followed by summing these products. The formula for calculating the relative atomic mass is as follows:
Relative Atomic Mass (Ar)=∑(Isotope Mass×Fractional Abundance)
Relative Atomic Mass (Ar)=∑(Isotope Mass×Fractional Abundance)
To put this formula into practice, consider an element X that has two naturally occurring isotopes: X-1 with a mass of 10 amu and an abundance of 75%, and X-2 with a mass of 11 amu and an abundance of 25%. The calculation would proceed as follows:
- Convert the percentage abundances into fractional values: 75% becomes 0.75, and 25% becomes 0.25.
- Multiply the mass of each isotope by its fractional abundance: (10 amu 0.75) + (11 amu 0.25).
- Sum these values to find the relative atomic mass: (7.5 amu) + (2.75 amu) = 10.25 amu.
Thus, the relative atomic mass of element X, considering its isotopic composition, would be 10.25 amu.
Practical Examples and Applications
To illustrate the practicality and importance of calculating relative atomic mass, let’s examine a real-world example involving the element chlorine. Chlorine has two primary isotopes:
35��
35
Cl with an approximate mass of 35 amu and an abundance of about 75.77%, and
37��
37
Cl with a mass of 37 amu and an abundance of 24.23%. Applying the calculation method:
- Convert percentages to fractions: 75.77% to 0.7577 and 24.23% to 0.2423.
- Multiply each isotope’s mass by its fractional abundance: (35 amu 0.7577) + (37 amu 0.2423).
- Sum these values: (26.5195 amu) + (8.9651 amu) = 35.4846 amu.
Therefore, the relative atomic mass of chlorine is approximately 35.485 amu, a value that is corroborated by its standard atomic weight listed in the periodic table.
This calculation is not just an academic exercise; it has practical implications in various scientific fields. In analytical chemistry, understanding the relative atomic mass is essential for accurate mass spectrometry analysis and in the determination of molecular formulas. In pharmaceuticals, it aids in the precise formulation of compounds and dosages. Environmental scientists rely on this calculation to understand isotopic distributions in ecological studies, and it is also crucial in the field of nuclear science for reactor design and understanding fission and fusion processes.
Theoretical Foundations and Implications
The calculation of relative atomic mass is deeply rooted in the atomic theory and the understanding of isotopes, developed through the work of scientists such as John Dalton, J.J. Thomson, and Francis Aston. The concept underscores the atomic structure and the binding forces within nuclei, providing insights into nuclear stability and the processes of radioactive decay.
Moreover, the relative atomic mass serves as a bridge between the microscopic properties of atoms and their macroscopic manifestations. It allows chemists to scale up from atomic-level phenomena to quantities that can be measured and manipulated in the laboratory, facilitating the transition from theoretical chemistry to practical applications.
Conclusion
The process of calculating relative atomic mass is a fundamental skill in chemistry, bridging the gap between atomic theory and practical chemical applications. By understanding and applying this concept, one gains not only the ability to perform essential calculations but also a deeper appreciation for the intricacies of atomic structures and the diversity of isotopes in nature. Whether for academic purposes, research, or practical applications in various scientific fields, mastering the calculation of relative atomic mass is an invaluable asset, illuminating the complexities of the chemical world and enhancing our ability to harness its principles for human benefit.